HyperLogLog算法 - GitPress.io

HyperLogLog简介

HyperLogLog算法简称HLL，作用是提供不精确的去重计数。存在以下特点：

代码实现较难
能够使用极少的内存统计巨量数据。例：在Redis中实现的HyperLogLog，仅需12K内存就能统计 2⁶⁴ 条数据
计数存在一定误差，且误差率整体较低。标准误差为 0.81%
误差可以通过设置辅助计算因子降低

问题原型

统计一个页面，每天有多少用户点击进入，相同用户的重复点击记为1次
- 解决方法：最直接的方法是使用HashMap这种数据结构，然而当用户数量达到百万或千万以上级别时，HashMap会导致大量的内存占用
- 估算：假设用HashMap<String, Bool>存储<id, 是否点击进入>。HashMap的内存占用空间为用户数量 * (String + Bool)

新的挑战

满足该需求还可以使用B+树，Bitmap位图，以及HyperLogLog算法，可以应对庞大的数据规模。HyperLogLog算法是一种借助概率论-伯努利实验的估算，因此需要考虑使用后是否在可容忍的误差范围内

伯努利实验

伯努利试验（Bernoulli trial）(或译为白努利试验)是只有两种可能结果（成功或失败）的单次随机试验，即对于一个随机变量X而言，

Pr[X = 1] = p
Pr[X = 0] = 1-p

而伯努利过程是一列独立同分布的伯努利试验。假设是抛硬币，记录每次伯努利过程直到抛出正面的次数为 k，那么必然有一个最大的抛掷次数 k_max，且易有以下结论：

n次伯努利过程的投掷次数都满足 k<=k_max
n次伯努利过程，至少有一次的投掷次数满足 k=k_max

结合极大似然估计的方法，可以发现在 n 和 k_max 中存在估算关联：n = 2^(k_max) 例：

第1次试验: 抛了3次才出现正面，此时 k=3，n=1
第2次试验: 抛了2次才出现正面，此时 k=2，n=2
第3次试验: 抛了6次才出现正面，此时 k=6，n=3
第n次试验：抛了12次才出现正面，估算 n=2^12

假设取上述例子前3组，那么此时 k_max=6, n=3，不满足估算公式 2^6≠3，因此需要足够多的实验次数才能保证估算的准确性，当实验次数不足时估算公式的误差很大

估算优化

当n足够大时，估算的误差率会相对减少，但是仍然不够小。

进行多轮试验，轮次记作 m，再取每轮的 k_max，再取平均数即 k_max/m，最终再估算 n 即 LogLog算法的做法
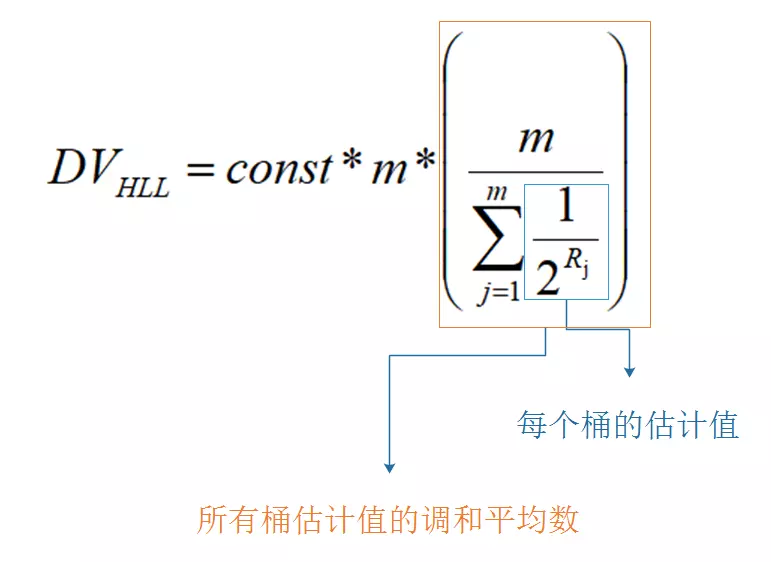
LogLog估算公式：
DV* _LL = constant * m * 2^R平均
上述公式的 DV _LL 对应的就是 n，constant 是修正因子，可按实际情况设置。m 代表的是试验的轮数，R平均 即算术平均数。

这种通过增加试验轮次，再取k_max平均数的算法优化就是LogLog的做法。而 HyperLogLog和LogLog的区别就是采用的不是平均数，而是调和平均数。调和平均数比平均数的优点在于不易受到大数值的影响。例：

A工资1000/月，B工资30000/月，求平均工资

算术平均数：(1000 + 30000)/2 = 15500
调和平均数：2/(1/1000 + 1/30000) ≈ 1935.484

调和平均数计算公式：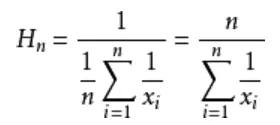

HyperLogLog与问题原型的关联

比特串

通过Hash函数可以将数据转为比特串，即转为二进制。转化后可以和试验中的抛硬币场景相对应，将比特串中的0视作反面，1视作正面。一个数据最终被转化为 10010000，那么从最低有效位(lsb)往最高有效位(msb)观察，首次出现1的时候就是正面。现在可以借助出现1的最大的位置 k_max 来估算共存储了多少数据

分桶

即分多少轮。抽象到计算机存储中，即存储的是一个单位是bit，长度是L的大数组S，将S平均分为m组，即m轮。每组所占的bit个数是平均的，设为P，易得：

L = S.length
L = m * p
以 K 为单位，S占用的内存 = L/8/1024

m=16834，p=6，L=16834 * 6。占用内存为 = 16834*6/8/1024 = 12K

  第0组     第1组                       .... 第16833组
[000 000] [000 000] [000 000] [000 000] .... [000 000]

对应

现在回到我们的原始APP页面统计用户的问题中去。

设 APP 主页的 key 为： main
用户 id 为：idn , n->0,1,2,3.... 类比每一个id转化后的比特串为一次伯努利试验，为了进行实现原试验中的分轮即分桶
可以假设对比特串做了切分，使用低2位计算桶标志，之前的位用于估算。例如某个用户id的比特串是：1000010010011。所在桶标志为： 11(2) = 1*2^1 + 1*2^0 = 3，用户估算的比特串是 10000100100，从lsb往msb观察，第一次出现1的位置是3。
综合起来，第3个桶，即第3次试验中，k_max = 3。3 对应的二进制是：11，因为每个桶有p个比特位。当p>=2时，即可存入11。

模仿上述流程，多个不同的用户 id，就被分散到不同的桶中去了，且每个桶有其 k_max。当要统计APP 主页有多少用户点击量的时候，就是一次估算。最终结合所有桶中的 k_max，代入估算公式，便能得出估算值。 HLL