Article Outline
算法简述
- 并查集是一种树形的数据结构,其保持着用于处理一些不相交集合(Disjoint Sets)的合并及查询问题。常在使用中以森林来表示,进行操作。
算法复杂度分析
- 时间复杂度 = O(1)
- N次合并M次查找的复杂度 = O(M α(N)),其中α是Ackerman函数的某个反函数,α的值域可视为<4的,即并查集操作可视为线性的。
- 空间复杂度 = O(n)
基本操作
- Find:确定元素属于哪一个集合。不要求find操作返回任何特定的名字,而只要求当且仅当两个元素属于相同的集合时,作用在这两个元素上的find返回相同的名字。
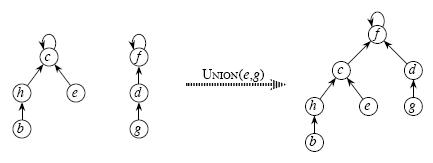
- Union:将两个子集合并成同一个集合
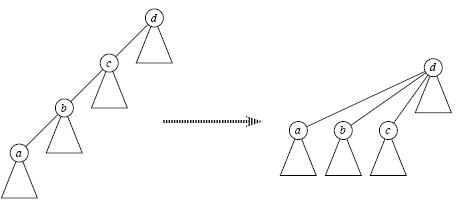
- Find:确定元素属于哪一个集合。不要求find操作返回任何特定的名字,而只要求当且仅当两个元素属于相同的集合时,作用在这两个元素上的find返回相同的名字。
#include<stdio.h>
const int maxn = 100;
int f[maxn] = {0};
int get(int v) {
if(f[v] == v) {
return v;
} else {
f[v] = get(f[v]);
return f[v];
}
}
void merge(int x, int y) {
int tx, ty;
tx = get(x);
ty = get(y);
if(tx != ty) {
f[ty] = tx;
}
return;
}
int main() {
int i, x, y, sum=0;
// n is group size, m is merge time
int n = 12, m = 5;
for(i = 1; i <= n; i++) {
f[i] = i;
}
for(i = 1; i <= m; i++) {
scanf("%d%d", &x, &y);
merge(x,y);
}
for(i = 1; i <= n; i++) {
if(f[i] == i) {
sum++;
}
}
printf("%d\n",sum);
return 0;
}