Kaggle 住宅価格予測 多項式回帰してみる

はじめに

今回は多項式を使って回帰分析したいと思います.
いままでの線形回帰では一次式(直線)の回帰式を求めていましたが, 多項式を使うことで曲線の回帰式を求めることができます.

準備

共通の処理です.

# ライブラリのインポート
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import numpy as np
from sklearn.linear_model import LinearRegression
from sklearn.preprocessing import StandardScaler

%matplotlib inline 

# trainデータ
train = pd.read_csv('./data/train.csv')
# データフレームに変換
df_train = pd.DataFrame(train)
# trainデータから説明変数と目的変数を取得
X = df_train.loc[:, ['OverallQual']].values
y = df_train.loc[:, ['SalePrice']].values

まず一次式で単回帰

最初に一次式で単回帰をして結果を確認します.

ホールド・アウト法でデータを分割して通常の線形回帰モデルで学習させます.

from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.3, random_state = 0)
reg = LinearRegression()
reg.fit(X_train, y_train)

データの分布と得られた回帰式からの予測をグラフにしてみます.

plt.scatter(X_train,y_train)
x = np.arange(0, 15, 1).reshape(-1, 1)
plt.plot(x, reg.predict(x),color='red')
plt.show()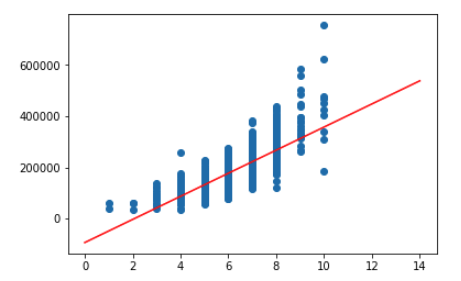

大体真ん中を通っていますね. 一次式のモデルを使ったのでもちろん直線の回帰式です.
最後に評価を見てみます.

# モデルの評価
print('R^2')
print('train: %.5f' % reg.score(X_train, y_train))
print('test: %.5f' % reg.score(X_test, y_test))

出力 R^2 train: 0.61489 test: 0.64792

test方が高いので過学習はしていません(それはそう)

二次式でやってみる

2次式の回帰式になるようにデータを基底変換します.

from sklearn.preprocessing import PolynomialFeatures
quad = PolynomialFeatures(degree=2)
X_quad = quad.fit_transform(X)

ホールド・アウト法でデータを分割

from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X_quad, y, test_size = 0.3, random_state = 0)

線形回帰モデルを使って学習.

model_quad = LinearRegression()
model_quad.fit(X_train, y_train)

データの分布と得られた回帰式からの予測をグラフに.

plt.scatter(overal_qual, y, color='lightgray', label='data')
x = np.arange(0, 15, 1).reshape(-1, 1)
x_quad = quad.fit_transform(x)
plt.plot(x, model_quad.predict(x_quad), color='green', label='quad')
plt.show()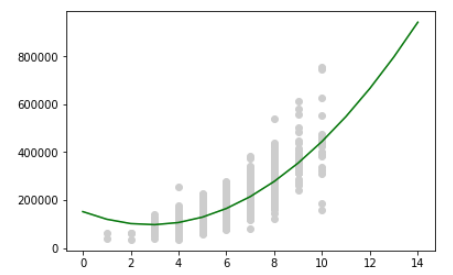

いい感じの曲線になっていますね.
一次式のときよりも予測結果がいい感じにはまっている気がします.
評価を見てみましょう.

# モデルの評価
print('R^2')
print('train: %.5f' % model_quad.score(X_train, y_train))
print('test: %.5f' % model_quad.score(X_test, y_test))

出力 R^2 train: 0.67123 test: 0.69228

一次式の回帰式のときよりも良い精度がでました.

まとめ

説明変数と目的変数に曲線的な相関があるときは2次や3次の回帰式を使うと予測がいい感じに当てはまります.
今回は単回帰にしてグラフでわかりやすくしましたが, 重回帰でも同様に行えます.
大体2次にしてたらいい感じになるのでわ...(