逻辑门

关于同一种逻辑门的名称和表述，本文只介绍最常见的一种或两种。没有列出的表述均为不常用或老旧的版本，如果见到应当留意。

其中，符号有两种。下面左图是ANSI及IEEE标准，右图是IEC标准。

---

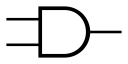
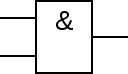
与门、或门、非门

首先是三种最基本的逻辑门：与门、或门、非门。

与门

英文名：AND
逻辑函数： $A\cdot B$
Verilog 表达式： $a&b$
性质：只有所有输入均为 1 时，输出为 1；若有任意输入为 0，输出为 0.
真值表：

A	B	A AND B
0	0	0
0	1	0
1	0	0
1	1	1

或门

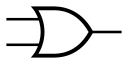
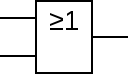
英文名：OR
逻辑函数： $A + B$
Verilog 表达式： $a|b$
性质：只有所有输入均为 0 时，输出为 0；若有任意输入为 1，输出为 1.
真值表：

A	B	A OR B
0	0	0
0	1	1
1	0	1
1	1	1

非门

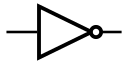
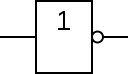
英文名：NOT
逻辑函数： $\overline{A}$
Verilog 表达式： $\sim a$
性质：输入为 1 时输出为 0 ，输入为 0 时输出为 1. 真值表：

A	NOT A
0	1
1	0

符号中的小泡泡表示“取非”，这点可以在后面的符号中见到。

与非门、或非门

这两种门可以看作在与门、或门之后再取非。逻辑函数的表达式也可以印证这一点。

与非门

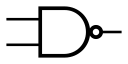
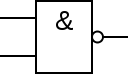
英文名：NAND
逻辑函数： $\overline{A \cdot B}$
Verilog 表达式： $\sim(a&b)$
性质：所有输入为 1 时输出为 0 ，其余情况输出为 1. 真值表：

A	B	A NAND B
0	0	1
1	0	1
0	1	1
1	1	0

或非门

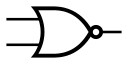
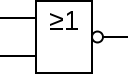
英文名：NOR
逻辑函数： $\overline{A+B}$
Verilog 表达式： $\sim(a|b)$
性质：所有输入为 0 时输出为 1 ，其余情况输出为 0. 真值表：

A	B	A NOR B
0	0	1
0	1	0
1	0	0
1	1	0

异或门、同或门

这两种门对于初学者会是比较独特的门。实际使用上，这些闸是由更基本的逻辑门组合成的。

异或门

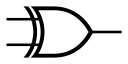
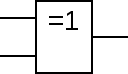
英文名：NOR （Exclusive-OR gate，又称EOR gate、ExOR gate） 逻辑函数： $A\oplus B = A\overline{B}+\overline{A}B$
Verilog 表达式： $a \wedge b$
性质：当两个输入相同时，输出 0；两个输入不同时，输出 1. 真值表：

A	B	A XOR B
0	0	0
0	1	1
1	0	1
1	1	0

符号 $\oplus$ 其实可以理解为 “模2和”，就是求和后除以2取余数；理解为二进制加法也是可以的。

同或门（异或非门）

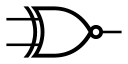
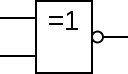
英文名：XNOR（偶尔写作ENOR gate、ExNOR gate）
逻辑函数： $A\odot B=AB+\overline{A}\overline{B}$
Verilog 表达式： $a\sim \wedge~ b$ 或 $\sim a\wedge b$
性质：当两个输入相同时，输出 1；两个输入不同时，输出 0. 真值表：

A	B	A XNOR B
0	0	1
0	1	0
1	0	0
1	1	1

等同于在异或门后加一个非门。

$$\overline{A \oplus B} = A \odot B$$ $$\overline{A \odot B} = A \oplus B$$

蕴含门、蕴含非门

蕴含门

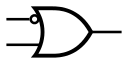
英文名：IMPLY
逻辑函数： $A\rightarrow B$
Verilog 表达式：尚未遇到
性质：如果第一输入为低时，输出高，否则输出与第二输入相同的高低状态。
真值表：

A	B	A IMPLY B
0	0	1
0	1	1
1	0	0
1	1	1

蕴含非门

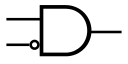
英文名：NIMPLY
逻辑函数： $\overline{A\rightarrow B}$
Verilog 表达式：尚未遇到
性质：如果第一输入为低时，输出低，否则输出与第二输入相反的高低状态。
真值表：

A	B	A NIMPLY B
0	0	0
0	1	0
1	0	1
1	1	0

是门

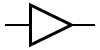
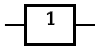
英文名：BUF
逻辑函数： $A$
Verilog 表达式：尚未遇到
性质：输出与输入相同。
真值表：

A	BUF A
0	0
1	1