HOME/Articles/

RとC++で二重振り子(double pendulum)

Author
統計ソフトRの備忘録３
Published
2021/06/10
Updated
2022/04/29
Rodeintrdouble pendulum
Article Outline

RとC++で二重振り子(double pendulum)

">Hits

今回の記事は、

  1. odeintrパッケージを使って二重振り子の微分方程式をC++でコンパイル。
  2. 二重振り子の動きをpngファイルで保存。
  3. ImageMagickを使ってアニメーションgifを作成。

なお、OSはlinuxです。

(参考)
thk686/odeintr
odeintr package

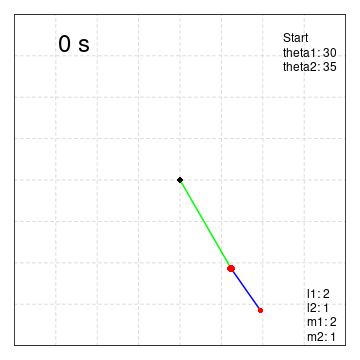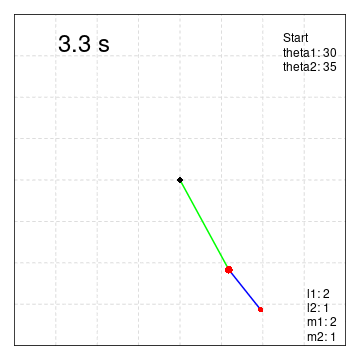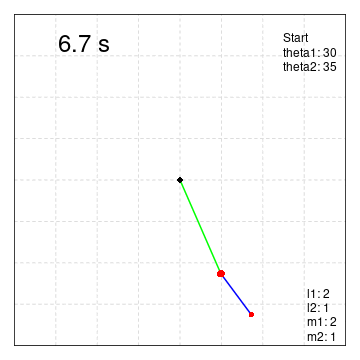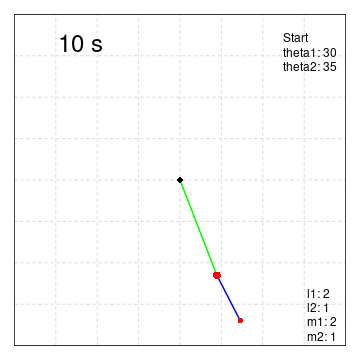
theta1:30° theta2:35°

pendulum3035

movie3035.gif

theta1:30° theta2: -35°

pendulum30_35

movie30_35.gif

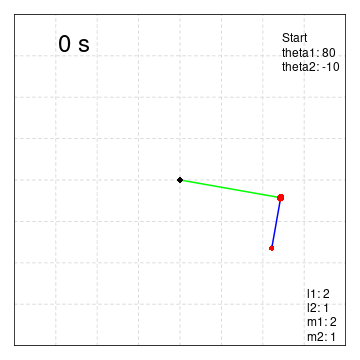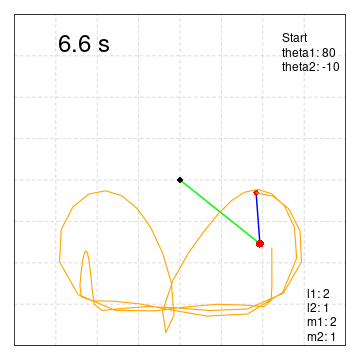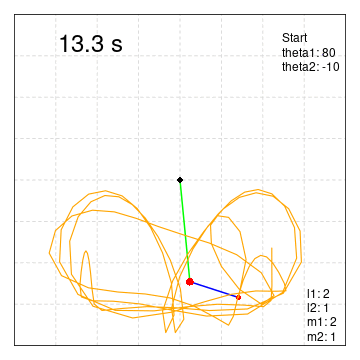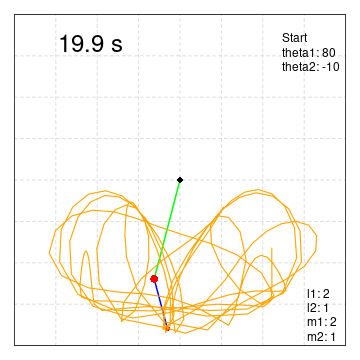
theta1:80° theta2: -10°

pendulum80_10

軌跡をつけた movie80_10.gif

Rcode

パッケージの読み込みとパラメータの設定

require(odeintr)
# 二重振り子
# l1,l2:錘をつなぐ棒の長さ　m1,m2:錘の重さ
parameters = c(l1=2 , l2=1 , m1=2 , m2=1 , g= 9.807)

odeintrパッケージを通してC++でコンパイルする微分方程式を記述する。

(注意)記法がR関数の記法とは違う。

  • theta1=x[0], theta2=x[1], velocity1=dxdt[0]=x[2], velocity2=dxdt[1]=x[3]
  • theta1の２階微分=velocity1の微分=dxdt[2] ,theta2の２階微分=velocity2の微分=dxdt[3]

関数の元になる微分方程式は以下の３つのサイトのものを使用させていただきました。（手抜きです。）
結果はどれを使っても同じです。 

#https://www.sejuku.net/blog/74879
doublependulum.sys ="
    dxdt[0]= x[2] ;
    dxdt[1]= x[3] ;
    dxdt[2]= (m2*l1*x[2]*x[2]*sin(x[1]-x[0])*cos(x[1]-x[0])+m2*g*sin(x[1])*cos(x[1]-x[0])+m2*l2*x[3]*x[3]*sin(x[1]-x[0])-(m1+m2)*g*sin(x[0]))/
        ((m1+m2)*l1-m2*l1*cos(x[1]-x[0])*cos(x[1]-x[0]));
    dxdt[3]= (-m2*l2*x[3]*x[3]*sin(x[1]-x[0])*cos(x[1]-x[0])+(m1+m2)*g*sin(x[0])*cos(x[1]-x[0])-(m1+m2)*l1*x[2]*x[2]*sin(x[1]-x[0])-(m1+m2)*g*sin(x[1]))/
        ((m1+m2)*l2-m2*l2*cos(x[1]-x[0])*cos(x[1]-x[0]));
"
# Espíndola_2019_J._Phys. _Conf._Ser._1221_012049.pdf
doublependulum.sys ="
    dxdt[0]= x[2] ;
    dxdt[1]= x[3] ;
    dxdt[2]= (-g*m1*sin(x[0])-g*m2*sin(x[0]-x[1])*cos(x[1])-cos(x[0]-x[1])*sin(x[0]-x[1])*l1*m2*x[2]*x[2]-sin(x[0]-x[1])*l2*m2*x[3]*x[3])
        /(l1*(m1+m2*sin(x[0]-x[1])*sin(x[0]-x[1])));
    dxdt[3]=(sin(x[0]-x[1])*(m1*(g*cos(x[0])+l1*x[2]*x[2])+m2*(g*cos(x[0])+l1*x[2]*x[2]+cos(x[0]-x[1])*l2*x[3]*x[3])))
        /(l2*(m1+m2*sin(x[0]-x[1])*sin(x[0]-x[1])));
"
# http://www.ne.jp/asahi/tokyo/nkgw/gakusyu/rikigaku/2zyufuriko/zyufuriko_kaisetu/zyufuriko_kaisetu.html
doublependulum.sys ="
    dxdt[0]= x[2] ;
    dxdt[1]= x[3] ;
    dxdt[2]= (-(m1+m2)*g*sin(x[0])+m2*g*cos(x[0]-x[1])*sin(x[1])-l1*m2*cos(x[0]-x[1])*sin(x[0]-x[1])*x[2]*x[2]-l2*m2*sin(x[0]-x[1])*x[3]*x[3])
        /(l1*(m1+m2*sin(x[0]-x[1])*sin(x[0]-x[1])));
    dxdt[3]=((m1+m2)*g*cos(x[0])*sin(x[0]-x[1])+l1*(m1+m2)*sin(x[0]-x[1])*x[2]*x[2]+l2*m2*cos(x[0]-x[1])*sin(x[0]-x[1])*x[3]*x[3])
        /(l2*(m1+m2*sin(x[0]-x[1])*sin(x[0]-x[1])));
"

コンパイル

compile_sys(name="doublependulum",sys=doublependulum.sys, pars=parameters, const=TRUE, method="rk4", compile=TRUE)

位置（角度）の初期値、終了時間、時間刻みを入力

theta1 = 80
theta2 = -10
duration = 20
step_size = 0.1

位置（角度）と角速度を計算

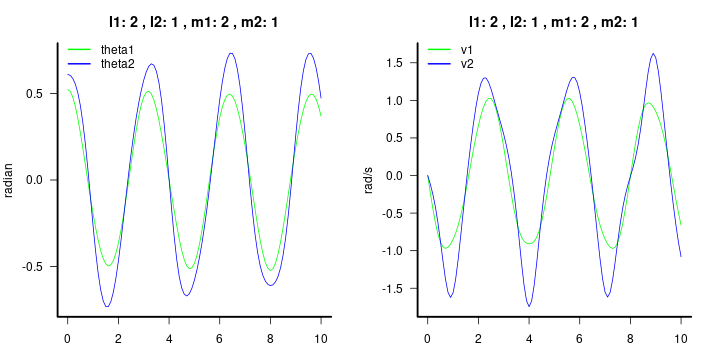
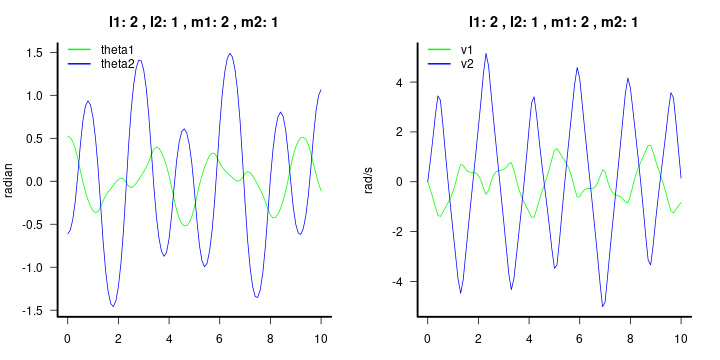
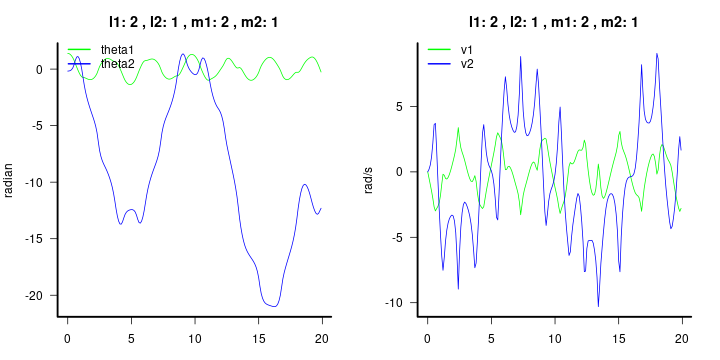
sol=doublependulum(c(theta1*pi/180,theta2*pi/180,0,0),duration=duration,step_size =step_size)

グラフ作成：経過時間と位置（角度）、経過時間と角速度。

# sol[,1]:経過時間 sol[,2]:theta1  sol[,3]:theta2  sol[,4]:velocity1  sol[,5]:velocity2
#png("pendulum01.png",width=720,height=360)
par(mar=c(3,4,3,2),mfrow=c(1,2))
plot(sol[,1],sol[,2],type="l",col="green",xlab="t",ylab="radian",ylim=c(min(sol[,2:3]),max(sol[,2:3])),bty="n",las=1)
box(bty="l",lwd=2.5)
lines(sol[,1],sol[,3],col="blue")
legend("topleft",inset=c(0,-0.03),legend=c("theta1","theta2"),lwd=2,col=c("green","blue"),bty="n",xpd=T)
title(paste("l1:",parameters[1] ,", l2:",parameters[2],", m1:",parameters[3] ,", m2:",parameters[4]))
#
plot(sol[,1],sol[,4],type="l",col="green",xlab="t",ylab="rad/s",ylim=c(min(sol[,4:5]),max(sol[,4:5])),bty="n",las=1)
box(bty="l",lwd=2.5)
lines(sol[,1],sol[,5],col="blue")
legend("topleft",inset=c(0,-0.03),legend=c("v1","v2"),lwd=2,col=c("green","blue"),bty="n",xpd=T)
title(paste("l1:",parameters[1] ,", l2:",parameters[2],", m1:",parameters[3] ,", m2:",parameters[4]))
par(mfrow=c(1,1))
#dev.off()

デカルト座標(x1,y1,x2,y2)に変換

# sol[,1]:経過時間   sol[,2]:theta1  sol[,3]:theta2
x1 <-  parameters[1]*sin(sol[,2])    # li*sin(theta1)
y1 <-  -parameters[1]*cos(sol[,2])
x2 <- parameters[2]*sin(sol[,3]) + x1
y2 <- -parameters[2]*cos(sol[,3]) + y1
# LL: l1 + l2
LL<- parameters[1]+parameters[2]

二重振り子の動きをpngファイルで保存。

for (i in 1:length(x1)){
png(paste0("./Pendulum/PendulumA",sprintf("%03d",i),".png"),width=360,height=360)
par(mar=c(1,1,1,1))
plot(NULL,xlim=c(-LL,LL),ylim=c(-LL,LL),xlab="",ylab="",las=1,axes=F,panel.first= grid(8,8,lty= 2,col= "lightgray"))
box()
segments(x0=0,y0=0,x1= x1[i],y1=y1[i],col="green",lwd=2)
segments(x0=x1[i],y0=y1[i],x1= x2[i],y1=y2[i],col="blue",lwd=2)
points(0,0,pch=16,cex=1)
points(x= x1[i],y=y1[i],col="red",pch=16,cex=sqrt(parameters[1]))
points(x= x2[i],y=y2[i],col="red",pch=16,cex=sqrt(parameters[2]))
legend("topleft",legend=paste(sol[i,1],"s"),bty="n",cex=2)
legend("topright",legend=paste("Start","\ntheta1:",theta1,"\ntheta2:",theta2),bty="n",cex=1)
legend("bottomright",inset=c(0,0.05),
    legend=paste("l1:",parameters[1] ,"\nl2:",parameters[2],"\nm1:",parameters[3] ,"\nm2:",parameters[4]),bty="n",cex=1)
dev.off()
}

ImageMagickを使ってアニメーションgifを作成

system("convert -delay 0.1 -loop 0 ./Pendulum/PendulumA*.png movie.gif")

二重振り子の動きをpngファイルで保存。(軌跡付き)

３行増やしただけです。

kiseki<- NULL
for (i in 1:length(x1)){
png(paste0("./Pendulum/PendulumK",sprintf("%03d",i),".png"),width=360,height=360)
par(mar=c(1,1,1,1))
plot(NULL,xlim=c(-LL,LL),ylim=c(-LL,LL),xlab="",ylab="",las=1,axes=F,panel.first= grid(8,8,lty= 2,col= "lightgray"))
box()
segments(x0=0,y0=0,x1= x1[i],y1=y1[i],col="green",lwd=2)
segments(x0=x1[i],y0=y1[i],x1= x2[i],y1=y2[i],col="blue",lwd=2)
points(0,0,pch=16,cex=1)
points(x= x1[i],y=y1[i],col="red",pch=16,cex=sqrt(parameters[1]))
points(x= x2[i],y=y2[i],col="red",pch=16,cex=sqrt(parameters[2]))
kiseki<- rbind(kiseki,data.frame(x2[i],y2[i]))
lines(kiseki[,1],kiseki[,2],lwd=1.5,col="orange")
legend("topleft",legend=paste(sol[i,1],"s"),bty="n",cex=2)
legend("topright",legend=paste("Start","\ntheta1:",theta1,"\ntheta2:",theta2),bty="n",cex=1)
legend("bottomright",inset=c(0,0.05),
    legend=paste("l1:",parameters[1] ,"\nl2:",parameters[2],"\nm1:",parameters[3] ,"\nm2:",parameters[4]),bty="n",cex=1)
dev.off()
}

ImageMagickを使ってアニメーションgifを作成

system("convert -delay 0.1 -loop 0 ./Pendulum/PendulumK*.png movieK.gif")
BACK TO TOP
© 統計ソフトRの備忘録３ 2019
Powered by GitPress.io
Sponsored by Quail.ink