Kaggle 住宅価格予測 重回帰分析してみる

はじめに

前回, 単回帰分析を使って予測したので, 今回は重回帰分析を行いたいと思います.

学習

# データの読み込み
train = pd.read_csv('./data/train.csv')
# データフレーム型に変換
df = pd.DataFrame(train)
# 欠損値をとりあえず平均値で埋める
df = df.fillna(df.mean())
# 相関係数の表示 絶対値をとって降順にソートする
df.corr().loc[:, ['SalePrice']].abs().sort_values('SalePrice', ascending = False)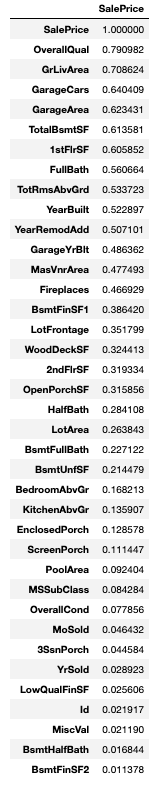

# 相関係数の高い上位3つを説明変数として取り出す
X = df.loc[:, ['OverallQual', 'GrLivArea', 'GarageCars']].values
# 目的変数を取り出す
y = df.loc[:, ['SalePrice']].values

# 標準化する
from sklearn.preprocessing import StandardScaler
ss = StandardScaler()
X = ss.fit_transform(X)

標準化は平均を0, 標準偏差を1に変換することです.
重回帰では複数の説明変数を使用するので標準化をして同じ単位にそろえる必要があります.

# ホールド・アウト法でデータを分割
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.3, random_state = 0)

ホールド・アウト法はデータをtrainとtestデータへ分割する方法です.
モデルの性能を測定するために用います.

# 線形回帰モデルを使う
from sklearn.linear_model import LinearRegression
lr = LinearRegression()
# trainデータを使って学習する
lr.fit(X_train, y_train)

# 自由度調整済み決定係数関数を定義する
def adjusted(score, n_sample, n_features):
    adjusted_score = 1 - (1 - score) * ((n_sample - 1) / (n_sample - n_features - 1))
    return adjusted_score

自由度調整済み決定係数を使ってモデルを評価します.

# モデルの評価
print('adjusted R^2')
print('train: %.3f' % adjusted(lr.score(X_train, y_train), len(y_train),X_train.shape[1]))
print('test : %.3f' % adjusted(lr.score(X_test, y_test), len(y_test), X_test.shape[1]))

出力 adjusted R^2 train: 0.748 test : 0.715

予測

# データの読み込み
test = pd.read_csv('./data/test.csv')
# データフレーム型に変換
df_test = pd.DataFrame(test)
# 欠損値をとりあえず平均値で埋める
df_test = df_test.fillna(df_test.mean())

# 説明変数を取り出す
X = df_test.loc[:, ['OverallQual', 'GrLivArea', 'GarageCars']].values
# 標準化する
X = ss.fit_transform(X)
# 予測する
y_pred = lr.predict(X)

# 配列を一次元に
y_pred = y_pred.flatten()
print(y_pred, y_pred.shape, type(y_pred))
# 提出ファイルの作成
test['SalePrice'] = y_pred
test[['Id','SalePrice']].to_csv('submission.csv',index=False)

結果

Scoreは 0.62264 でした.

おわりに

重回帰の場合では単回帰と違い, 標準化が必要です.
また自由度調整済み決定係数を使用してモデルの評価をします.

回帰の流れについて大体勉強できたので良かったです.
次は多項式回帰やGridSearch, ノルムについても書きます.